El algoritmo es tal como sigue:
- Generar dos números primos distintos, $p$ y $q$, que de preferencia sean "fuertes", es decir, strong prime. Estos dos números se multiplican para crear un nuevo número, $n$. En síntesis, $n = p * q$.
- Se calcula $\phi(n) = (p - 1)(q - 1)$ y se escoge al azar un número $e$ que sea relativamente primo a $\phi(n)$. Es decir, $gcd(e, \phi(n)) = 1$.
- Se calcula el inverso de $e$ con el módulo $\phi(n)$, es decir, un número $d$ tal que satisfaga la siguiente congruencia: $ed \equiv 1 \mod \phi(n)$.
- La llave pública es $(e, n)$, mientras que la llave privada es $(d, n)$. Uno nunca debe compartir $d$ ni $\phi(n)$ con nadie. La seguridad del algoritmo radica en la dificultad para factorizar $n$, pues para números realmente grandes no es una tarea fácil de realizar.
Si $M$ es un mensaje, se puede encriptar dicho mensaje con las llaves generadas de la siguiente manera: $C = E(M) = M^e \mod n $. Para recuperar el mensaje original, se debe desencriptar $C$ de tal manera que: $M = D(C) = C^d \mod n$. Si se observa con cuidado se puede notar que la operación es la misma, lo único que cambia es el orden en que se utilizan las llaves.
Por lo general, el orden presentado anteriormente se realiza para encriptar mensajes que serán enviados a otros usuarios, ¿pero qué pasaría si primero el mensaje se encripta con la llave privada del emisor y luego se vuelve a encriptar con la llave pública del destinatario? A esto se le conoce como firmas digitales, que es un mecanismo que se utiliza para tener una "forma" de poder identificarse con otros usuarios. El proceso de firmar un mensaje y enviarlo a otro usuario, quien a su vez deberá desencriptar el mensaje y verificar la firma, se ilustra así (los usuarios de prueba son llamados Alice y Bob para estos fines):
- Alice firma un mensaje $M$ con su llave privada: $C_{1} = M^d \mod n$.
- Alice encripta $C_{1}$ con la llave pública de Bob: $C_{2} = C_{1}^e \mod n$.
- Alice envía $C_{2}$ a Bob.
- Bob desencripta $C_{2}$ con su llave privada: $C_{1} = C_{2}^d \mod n$.
- Bob desencripta $C_{1}$ con la llave pública de Alice: $M = C_{1}^e \mod n$.
Como tarea se pidió crear un sitio web que funcionara como un repositorio de llaves públicas RSA. Para dicho propósito, se implementó en PHP, JavaScript y Python distintas funciones que realicen las siguientes actividades:
- Generación de llaves públicas y privadas.
- Función para encriptar y desencriptar llaves RSA.
- Mecanismos de verificación de la identidad del cliente y del sistema.
- Mecanismo de registro al repositorio.
Hay que dar click en este enlace para entrar al repositorio. A continuación se presentará casos de uso de la plataforma:
Si no estás registrado en el sistema, puedes hacerlo en el enlace de "Registro".
¿Preocupado por generar llaves? No te preocupes, el sistema lo realiza de manera automática. Cuando están llenos todos los campos hay que dar click en el botín de "Registro". Nota: d no se guarda en ningún lado.
Cuando se registra un nuevo usuario se regresa a la pantalla anterior. Ahora si es posible entrar al sistema :P Para entrar al sistema es necesario que el sistema genere un reto, dicho reto deberá ser computado en un script de Python que se descarga por separado. Nota: no implementé un mecanismo de descarga, perdón por las molestias.
Ya que se ha bajado el script, se ejecuta como se muestra en la pantalla. Los números que se envía al script son el reto, la d del usuario y su respectiva n. El número que computa el script es enviado al sistema en el campo "Respuesta". En el listado de usuarios se selecciona nuestro usuario y se da click en el botón "Entrar". Nota: si no aparece tu usuario en el listado después de que te registraste, actualiza la página.
Cuando llegamos a esta página el sistema desencripta nuestra respuesta, que en teoría, debe ser igual a la "respuesta" que el sistema puede computar. Si son iguales las respuestas, entonces se verifica nuestra identidad.
En caso de que el usuario "eligió" una respuesta equivocada, las respuestas obviamente no van a coincidir.
Si no es la primera vez que entras al sistema, se te hace una bienvenida con un mensaje de cuando fue la última vez que entraste.
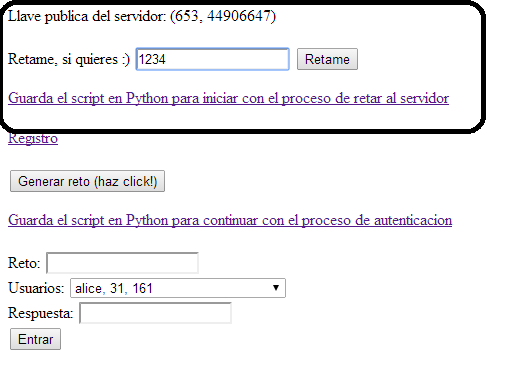
¿Tienes la sospecha que el sistema es falso? No te preocupes, también puedes retarlo para que verifique su identidad. Para realizar eso hay que descargar el script de Python indicado en la página de "Inicio", además de que hay que "generar" un reto para que el sistema lo compute. El reto lo introduce el usuario en la caja de texto, puede ser cualquier número entero positivo.
El sistema nos responde con un número. Este número es importante para verificar al sistema con el script de Python.
¿Qué pasa si nuestro reto es un número más grande que el n del sistema? No pasa nada, el sistema realiza un módulo con dichos números para evitar tener que volver a introducir otro número. El usuario humano no tiene porque preocuparse por eso, aunque si hay que indicarlo para evitar confusiones.
¿Qué pasa si nuestro reto es un número más grande que el n del sistema? No pasa nada, el sistema realiza un módulo con dichos números para evitar tener que volver a introducir otro número. El usuario humano no tiene porque preocuparse por eso, aunque si hay que indicarlo para evitar confusiones.
Para ejecutar el script se necesita enviar el reto, la respuesta que mostró el sistema, la e del sistema y su respectiva n. Si coincide los resultados, entonces el sistema confirma su identidad. Se observa que si se cambia tan solo un número de al menos uno de los argumentos el mensaje recuperado cambia drásticamente.
Generador de llaves
Se crean las llaves públicas y privadas con JavaScript. Por motivos de tiempo la generación de números primos es básica, aunque en Python ya tengo implementada una función para generar números primos fuertes.
Función para encriptar y desencriptar
No hay mucho que ver en esta función, porque es la misma tanto para encriptar como para desencriptar.
Identificación del cliente
No me gusta mucho PHP... cuando hay muchas instrucciones comienza a hacerse muy grande. El sistema computa $f(x)$ y desencripta la respuesta del usuario. Si estos son iguales, entonces el usuario completa su identificación.
Identificación del sistema
El proceso es un poco parecido que en la identificación del cliente, aunque ocurre en una aplicación de Python.
Mecanismo de registro
También este código es un poco confuso, pero básicamente incluye una llamada al generador de llaves y al mecanismo de registro en la base de datos, así como a algunos verificadores de campos.
Este fue un proyecto muy interesante y a la vez muy complejo, porque involucra muchos "módulos" y mecanismos que tienen que interactuar para llegar a un bien común. Para la próxima vez creo que es mejor empezar a trabajar con las funciones más básicas pero teniendo en cuenta el diseño global de la aplicación.
References
[1] Bruce Schneier "Applied Cryptography", 1996









+ key generation implemented and explained
ResponderEliminar+ users can register to the service
+ encryption/decryption implemented and explained
+ the server is authenticated
+ the user is authenticated
+ the service content distinguishes among users
+ adequate example runs
=> 7 out of 7 possible
Comments:
Errores de ortografía en el web service.
La bibliografía podría mejorarse, incluyendo las fuentes sobre python, php, etc., que seguramente consultaste durante el desarrollo de la tarea, pero esta vez lo dejo como advertencia sin multa.